NeuPDE

Hard-coding derivative to reduce the parameter count in NeuralODE

1. 

   NeuPDE: Neural network based ordinary and partial differential equations for modeling time-dependent data

   Yifan Sun, Linan Zhang, and Hayden Schaeffer

   In Mathematical and Scientific Machine Learning, 2020

   HTML Blog

TLDR: The paper introduces NeuPDE, a NeuralODE that uses polynomial features and discrete spatial derivative, with a shallow MPL

Insider's notes: It was not clear why this approach is relevant because they don't show the semantics of what is learned, nor get huge benefits (slightly less parameters, similar/worse accuracy, no variance, no code)

Context: In a NeuralODE style (where we want to learn to predict the velocity field, i.e., \(\dot{x}(t)\)), this paper aims at learning more constrained dynamics, enforcing derivative constraints.

Proposed solution: NeuPDE is a NeuralODE that uses a shallow MLP built on hard-coded derivative and correlation features. For time-series data, the model is fed with supervision at each individual time steps.

The architecture is restricted to an (untrained) polynomial feature transform \(\mathcal{D}(t, x)\) (e.g. polynomial features in sklearn), followed by a shallow MLP (two layers with just an ELU activation on the first). For spatio-temporal data, the spatial derivative are used instead of the polynomial features.

Let’s focus on one of the main equation of the paper, which is its optimization problem:

\[\operatorname*{min}_{\theta} \sum_{i=1}^{N}\ L(x(t_{i}))+\beta_{1}r(\theta) +\frac{\tilde{\beta}_{2}}{2}\sum_{i=0}^{N-1}||x(t_{i+1})-x(t_{i})||_{\ell^{2}}^{2}\] \[s.t.\ \ \ x(t_{0})=x_{0},\ \ \ x(t_{i})=\Phi^{(i)}(x(t_{0}),F(D(N(-)),\theta))\]

Where:

• the \(\beta\) values are set (without tuning),
• the loss \(L\) is for instance a \(\ell^2\) loss with the observed \(\tilde{x}_i\) (supposed observed),
• \(r(\theta)\) is a reguralization, using the \(\ell^1\) norm to encourage sparsity,
• \(F\) is the function that depends on the parameters to be learned \(\theta\),
• \(D\) is the previously defined feature transform,
• \(N\) is a min-max normalization that brings values to \(\left[-1, 1\right]\),
• the constrains are enforced by having the \(x(t_i)\) being generated using a integrator (ODE solver), with initial conditions set to \(x_0\).

The integrator that is used is based on RK (Runge Kutta), with one adaptative version called RK45 (or Runge-Kutta-Fehlberg?). We were wondering how equation (2) to cope for an adaptive time step, this element being further discussed in remark 2.2 about a continuous depth version that is reported to give similar results. In the discussion section, it is mentioned that RK (RK4 or RK45) is not necessary for image classification.

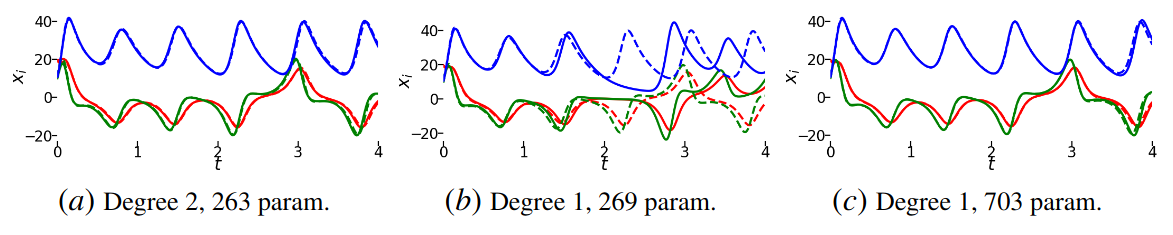
• Pros:
  • Less parameters are used.
  • The model is more constrained than a simple NeuralODE.
• Cons:
  • No interpretable representation seems to be extracted, while the paper aims at identifying an accurate governing differential structure.
    • We could not find the code related to the publication.
  • It is unclear how significant the results are.