Neural operators and chaotic attractors
Training neural operators to preserve invariant measures of chaotic attractors
Context: In chaotic systems, making long-horizon predictions is challenging because small perturbations in initial conditions cause trajectories to diverge at an exponential rate. Hence, training neural operators to minimize the MSE in prediction yields degenerate results over long time horizons which do not reproduce the statistical or structural properties of the dynamic.
Proposed solution: In this work, the authors propose to train neural operators on noisy data, taking as input an initial state and outputting future states in a recurrent fashion. To ensure that the trained neural operator respects the statistical properties of the chaotic dynamics, they suggest two learning strategies based on two distinct losses.
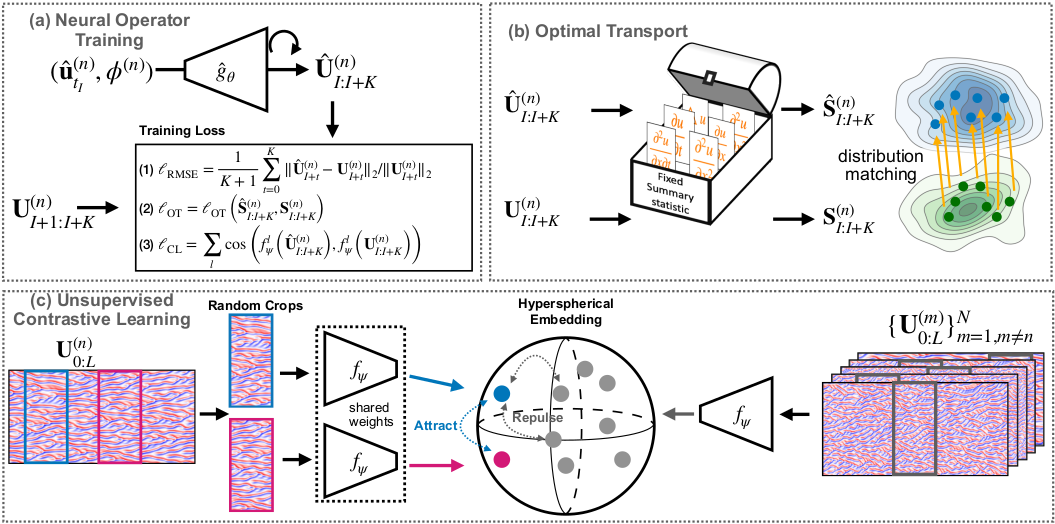
Firstly, they propose a physics-informed loss where some prior knowledge about invariant measures of the chaotic attractors (hereafter called summary statistics) is used. More specifically, they resort to an optimal transport-based loss (i.e., regularized Wasserstein distance) to match the distributions of a set of summary statistics between the data and the model prediction.
Secondly, in the absence of prior knowledge, they use unsupervised contrastive learning to learn relevant summary statistics. To achieve this, they first train an encoder from a sequence of data in order to capture invariant statistics of the dynamics. Then, they leverage the feature map of the encoder to construct a feature loss based on cosine similarity to preserve such invariant statistics during the training of the neural operator.
