Efficient Dynamics Modeling in Interactive Environments with Koopman Theory
Using Koopman theory to learn a linear dynamics in a latent space
Context: Modeling non-linear dynamics is difficult but useful in many contexts, including but not limited to RL (reinforcement learning, the domain of interest of this preprint).
Proposed solution: In this work, the authors propose to leverage the Koopman theory that says that any (nonlinear) dynamical system can be linearized in a high-dimensional latent space. The latent space is of possibly infinite dimensional but only a finite number are actually necessary to represent the dynamics with enough accuracy. This is especially true in the context of finite “training” sets. The mapping between the original space and the latent space can thus be approximated by a deep neural network, basically learning an auto-encoder.
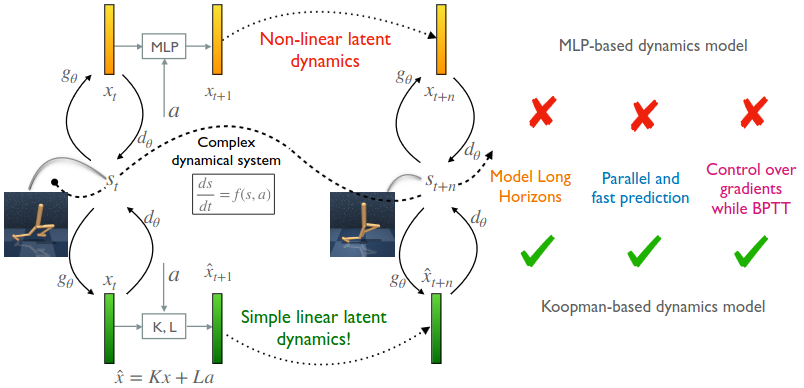
Some notes
- the term “observable” (coming from the Koopman theory) actually refers to the latent space
- the paper works with reinforcement learning so the dynamics involves a (diagonalized) transition matrix \(K\) but also an action encoder \(L\) (which would not exist in an non-RL setting)
- the paper discusses (Appendix D) the relation to DSSM (diagonal state space models)
One key point of the theory is that any matrix (so any linear dynamics / state transition) can be diagonalized, provided we consider values in the complex domain. The paper is actually focusing on RL but references previous work that do the same thing outside RL.
Predicting several time steps forward requires to compute powers of the \(K\) diagonal matrix. The they compute the (complex-valued) Vandermonde matrix containing the first \(\tau\) powers of the \(m\) eigenvalues. To consider the effect of successive the “inputs” (actions) they need to do a convolution of this Vandermonde matrix with the encoded actions, convolution that they do in the Fourier space.
