MeshFreeFlowNet

A Physics-constrained super-resolution framework

1. 

   MeshfreeFlowNet: A Physics-Constrained Deep Continuous Space-Time Super-Resolution Framework

   Chiyu Jiang, Soheil Esmaeilzadeh, Kamyar Azizzadenesheli, and 6 more authors

   In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, 2020

   HTML Blog Code

TLDR: The paper introduces MeshfreeFlowNet, a deep learning-based super-resolution framework to generate continuous grid-free spatio-temporal solutions from the low-resolution inputs

Insider's notes: REm[[[What happens if we do not pass the (relative) position to the second learned network? It might end up to be as accurate but with no computational drawback?]]]

Context: The aim is to proficiently depict high-resolution outputs and facilitate the integration of physical constraints, expressed as Partial Differential Equations (PDEs).

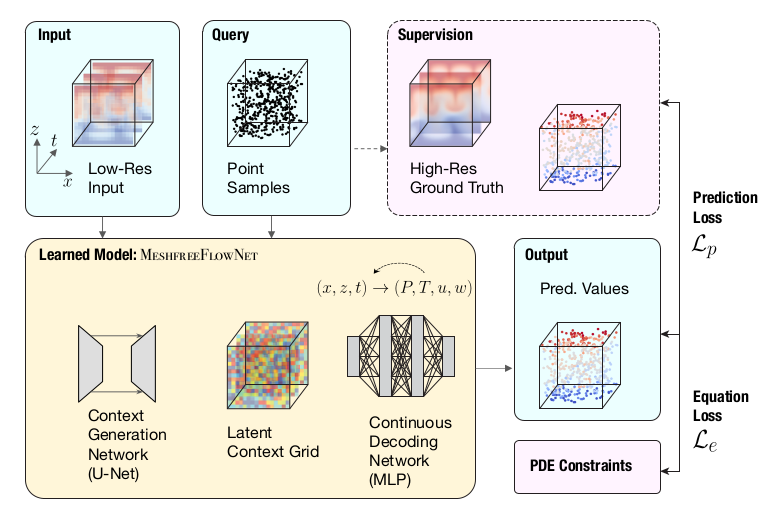
Proposed solution: MeshfreeFlowNet consists of two end-to-end trainable sub-networks, namely the Context Generation Network \(\Phi_{\theta_1}\) and the Continuous Decoding Network \(\Phi_{\theta_2}\), of parameters \(\theta_1\) and \(\theta_2\), respectively. The former produces a Latent Context Grid, by using a variant of the U-Net architecture, from a low-resolution physical input. Conversely, the latter generates physical quantities by means of a Multilayer Perceptron taking as input the concatenation of some context vector and a spatio-temporal coordinate. In order to generate physical quantities \(y_i\) at some high-scale coordinate \(x_i\), a trilinear interpolation of the output of the decoder is made :

\[\begin{equation} y_i =\sum_{j \in \mathcal{N}_i} w_j \Phi_{\theta_2}\left(\frac{x_i-x_j}{\Delta x}, c_j\right) \end{equation}\]

where \(\mathcal{N}_i\) is the set of neighboring vertices that bound \(x_i\), \((x_j,c_j)\) are the spatio-temporal coordinates and the latent context vector for the \(j\)-th vertex of the low-resolution grid, and the \(w_j\)’s are interpolation weights.

The parameters of the sub-networks are learned by minimizing a weighted combination of the PDE residual \(\mathcal{L}_e\) and the prediction error \(\mathcal{L}_p\), both evaluated at the high-scale resolution.

• Pros:
  • One can resort to autodifferentiation techniques to compute the PDE residual. since the spatio-temporal coordinates explicitly appear as inputs of the decoder.
• Cons:
  • For each query point \(x_i\), one needs to performs \(\|\mathcal{N}_i\|\) passes.